探索Java中的水仙花数：3种实现方式与性能对比

admin 2025-06-26 阅读:13 评论:0

在数学的海洋中，有一种特殊的数字被称为水仙花数（Narcissistic Number），也称为自幂数或阿姆斯壮数。这类数字在编程练习和算法学习中具有重要地位，尤其对于Java初学者来说是绝佳的练手项目。本文将全面剖析Java水仙花数的原理...

在数学的海洋中，有一种特殊的数字被称为水仙花数（Narcissistic Number），也称为自幂数或阿姆斯壮数。这类数字在编程练习和算法学习中具有重要地位，尤其对于Java初学者来说是绝佳的练手项目。本文将全面剖析Java水仙花数的原理、实现方法及优化技巧，带您领略数学与编程的完美结合。

一、水仙花数的数学原理

水仙花数是指一个n位数（n≥3），它的每个位上的数字的n次幂之和等于它本身。例如，153是一个典型的水仙花数，因为：1³ + 5³ + 3³ = 1 + 125 + 27 = 153。

探索Java中的水仙花数：3种实现方式与性能对比

数学特性分析：
1. 水仙花数都是自然数
2. 最小的水仙花数是153（3位数）
3. 不存在2位的水仙花数
4. 水仙花数相对稀少，4位数中只有3个

探索Java中的水仙花数：3种实现方式与性能对比

二、Java基础实现

2.1 基本判断方法

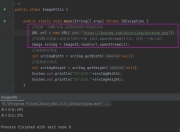
public class NarcissisticNumber {
    public static boolean isNarcissistic(int num) {
        if (num < 100 || num > 999) return false;

        int original = num;
        int sum = 0;

        while (num > 0) {
            int digit = num % 10;
            sum += Math.pow(digit, 3);
            num /= 10;
        }

        return sum == original;
    }
}

2.2 查找指定范围内的水仙花数

public static void findInRange(int start, int end) {
    System.out.println("水仙花数：");
    for (int i = start; i <= end; i++) {
        if (isNarcissistic(i)) {
            System.out.println(i);
        }
    }
}

三、高级实现与优化

3.1 支持任意位数的通用算法

public static boolean isNarcissisticAdvanced(int num) {
    if (num < 100) return false;

    String s = Integer.toString(num);
    int length = s.length();
    int sum = 0;

    for (char c : s.toCharArray()) {
        int digit = Character.getNumericValue(c);
        sum += Math.pow(digit, length);
    }

    return sum == num;
}