Java回文数检测终极指南：从基础算法到高级优化

admin 2025-06-26 阅读:11 评论:0

在编程面试和算法练习中，回文数判断是一个经典问题。本文将全面解析Java中判断回文数的各种方法，从基础实现到高级优化，帮助开发者掌握这一重要技能。什么是回文数？回文数是指正读和反读都相同的数字。例如121、1331、12321都是典型的回...

在编程面试和算法练习中，回文数判断是一个经典问题。本文将全面解析Java中判断回文数的各种方法，从基础实现到高级优化，帮助开发者掌握这一重要技能。

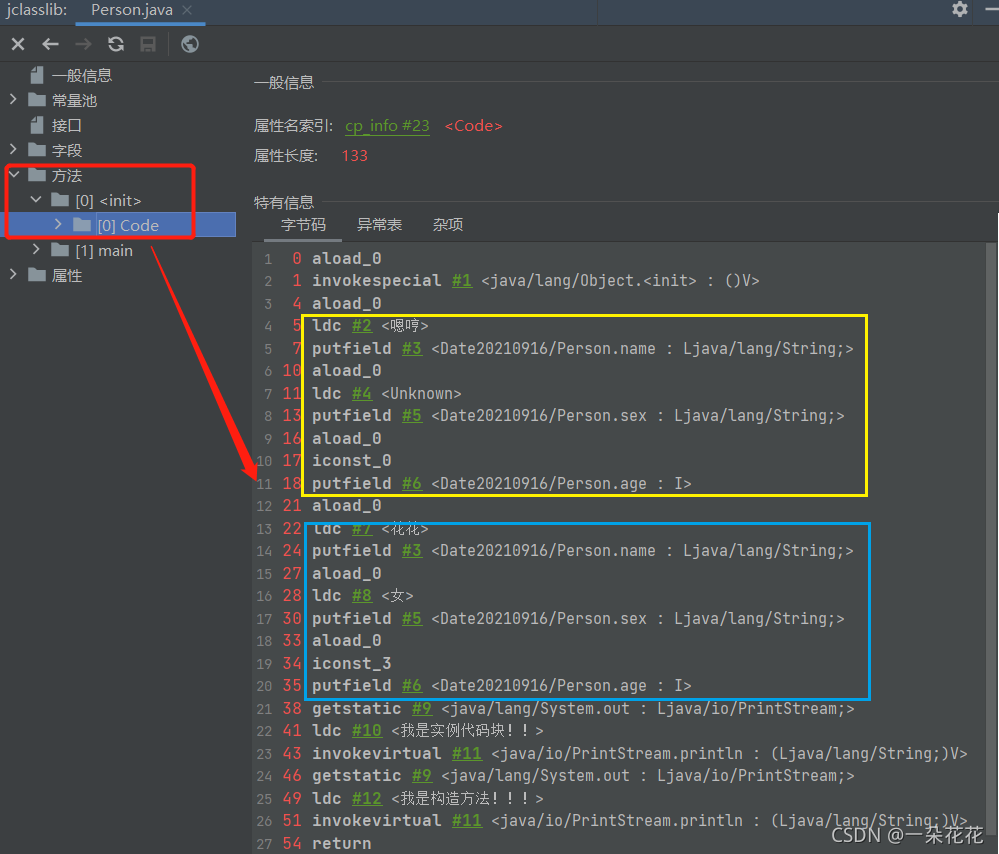
什么是回文数？

回文数是指正读和反读都相同的数字。例如121、1331、12321都是典型的回文数。判断一个数字是否为回文数是编程面试中的常见问题，也是检验基础算法能力的好方法。

方法一：字符串反转法

最直观的方法是将数字转换为字符串，然后反转比较：

public static boolean isPalindromeString(int x) {
    if (x < 0) return false;
    String str = Integer.toString(x);
    return str.equals(new StringBuilder(str).reverse().toString());
}

这种方法简单易懂，但存在性能问题：
1. 需要额外的字符串转换开销
2. 创建了多个临时对象
3. 时间复杂度为O(n)，空间复杂度为O(n)

方法二：数学反转法

更高效的做法是使用数学方法反转数字：

public static boolean isPalindromeMath(int x) {
    if (x < 0 || (x % 10 == 0 && x != 0)) return false;

    int reversed = 0;
    int original = x;

    while (x > 0) {
        reversed = reversed * 10 + x % 10;
        x /= 10;
    }

    return original == reversed;
}

优点：
1. 不需要额外空间
2. 时间复杂度O(log10(n))
3. 避免了字符串操作的开销

方法三：优化版数学反转

我们可以进一步优化，只反转一半数字：

public static boolean isPalindromeOptimized(int x) {
    if (x < 0 || (x % 10 == 0 && x != 0)) return false;

    int reversed = 0;
    while (x > reversed) {
        reversed = reversed * 10 + x % 10;
        x /= 10;
    }

    return x == reversed || x == reversed / 10;
}

这种优化：
1. 减少了一半的循环次数
2. 避免了整数溢出的风险
3. 保持了O(log10(n))的时间复杂度

方法四：双指针法

对于非常大的数字，可以考虑双指针法：

public static boolean isPalindromeTwoPointer(int x) {
    if (x < 0) return false;

    char[] digits = Integer.toString(x).toCharArray();
    int left = 0, right = digits.length - 1;

    while (left < right) {
        if (digits[left++] != digits[right--]) 
            return false;
    }
    return true;
}

适用场景：
1. 需要处理极大数字时
2. 内存不是主要限制因素
3. 代码可读性要求高

方法五：位运算技巧（仅限特定情况）

对于特定范围内的数字，可以使用位运算技巧：

Java回文数检测终极指南：从基础算法到高级优化

public static boolean isPalindromeBit(int x) {
    if (x < 0) return false;

    int mask = (int) Math.pow(10, (int) Math.log10(x));

    while (x > 0) {
        if (x / mask != x % 10) 
            return false;
        x = (x % mask) / 10;
        mask /= 100;
    }
    return true;
}